| Issue |
Europhysics News
Volume 56, Number 3, 2025
Soft matter physics
|
|
|---|---|---|
| Page(s) | 24 - 27 | |
| Section | Features | |
| DOI | https://doi.org/10.1051/epn/2025310 | |
| Published online | 31 July 2025 | |
Grains with different shape: what flows better, beads, rice or lentils?
Department of Complex Fluids, HUN-REN Wigner Research Centre for Physics Budapest Hungary
We can often observe that particles with slightly elongated or flat shape develop orientational ordering during flow. Does this result in an increased flowability of the material?
© European Physical Society, EDP Sciences, 2025
Granular flows are ubiquitous in nature and in various industrial applications [1]. We have all poured rice, peas, lentils or beans in our kitchen, grains representing different shape aspect ratio, and we might have wondered what role the shape of those grains plays in different flow configurations. The typical aspect ratio of rice grains varies between 2-5, while lentils are characterized by a number of 0.4, and industrial materials can be produced in any form, depending on the process. In order to answer the above question, we can think of various flow geometries. We can think about measuring the resistance of the granular material against shear deformation, or we can test which type of material flows out faster from a silo or clogs with higher probability when flowing through a constriction.
Rheology: fluids vs. granular materials
For the flow of common liquids – in a first approximation – the shear stress σ is proportional to the shear rate γ̇, but it is independent of pressure. Therefore the resistance of the material against shearing is characterized by the viscosity, which is defined as η=σ/γ̇. In a granular material all grains interact with their neighbors through frictional contacts with a particle friction coefficient of μp1. Thus, in a slow flow we have to consider the nature of dissipation on sliding contacts. As a result, for slow granular flows – in a first approximation – the shear stress σ is proportional to the pressure p, and it is independent of shear rate. Therefore, for characterizing the dissipation in slow granular flows, researchers define a so called effective friction, which is the ratio of shear stress and the local pressure μeff=σ/p [1].
Thus, we can characterize the grain shape dependence of the material’s resistance against shearing by measuring the effective friction μeff as a function of shape anisometry. For simple non-spherical shapes, such as ellipsoids or spherocylinders (cylinders with spherical caps), this is possible both in numerical simulations and in laboratory experiments.
Numerically, researchers often use particle based Discrete Element Models (DEM), where frictional particle-particle contacts can be modeled with reasonable approximations. In such simulations one can simply shear the granular material in a pressure controlled geometry, and measure the effective friction for systems with different grain shapes. In experiments, it is convenient to use the so called cylindrical split bottom shear cell, where a shear zone is generated (see red region on Fig. 1b). This is done by slowly rotating the middle part of the system using a rotating plate below the granular layer, while the outer part is at rest. In this case, the resistance of the system against shearing is measured by measuring the torque which is needed to maintain a stationary rotation of the middle part of the sample.
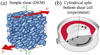 |
Fig. 1: (a) Schematic view of a granular material consisting of spherocylinders exposed to simple shear in a pressure controlled Discrete Element Model (DEM) calculation and (b) sketch of the cylindrical split bottom shear cell, in which the granular material is slowly sheared in the shear zone (indicated with red color). |
Elongated particle in a sheared liquid – Jeffery rotation
Considering an elongated particle placed in a sheared liquid (see Fig. 2), we find that for laminar flow the particle rotates (tumbles) with a periodically modulated rotation rate as described by Jeffery more than 100 years ago [2]. The particle rotates faster when its long axis is parallel to the flow gradient (∇ν), and slower when its long axis is parallel to the flow direction (ν). Thus, in a dilute suspension of rods subjected to shear flow – without any interaction between the particles – this already results in a shear alignment of the rods, since they spend more time parallel to the flow direction.
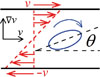 |
Fig. 2: Illustration of the rotation (tumbling) of an ellipsoidal particle in a liquid which is exposed to laminar shear flow with smooth (linear) velocity profile. |
Dry dense granular flow – interacting grains
In a dense granular flow random collisions between neighboring particles slightly modifies the picture described above, and leads to a noisy character of the rotation of the tumbling particle. This results in a modified orientation distribution, where the average orientation of the particles slightly deviates from the flow direction (see Fig. 3a). Decreasing particle aspect ratio leads to weaker orientational ordering, but stronger deviation of the alignment from the flow direction (Fig. 3b) [3].
 |
Fig. 3: (a) Orientation distribution of rice grains with different aspect ratio obtained in shear experiments. (b) Average angle of elongated particles as a function of particle aspect ratio in a dense granular shear flow [3]. Experimental data obtained on the surface of the granular layer or inside by X-ray computed tomography (CT). |
Effective friction vs. grain aspect ratio
How does then the complex grain dynamics observed in a shear flow for elongated particles affect the effective friction of the granular material compared to the case of spherical particles? The answer to this question is not simple. Numerical (DEM) simulations with spherocylinders have shown, that for typical frictional particles (μp>0.3) the effective friction μeff increases with particle aspect ratio [4], thus more elongated grains show larger resistance against shearing than less elongated or spherical ones (Fig. 4a). However, the shape dependence of the effective friction μeff becomes more complex for slippery particles (friction coefficient μp<0.3), for which non-monotonic curves are observed both in DEM simulations (Fig. 4a) and in laboratory experiments with plastic (POM) ellipsoids with smooth surface (Fig. 4b). In the experiments both rice-like and lentil-like ellipsoids were tested and similar behavior was observed: granular materials consisting of slightly anisometric particles (aspect ratios about 2 and 0.5) show stronger resistance against shear deformation than materials consisting of spheres or very anisometric particles [5].
 |
Fig. 4: (a) Effective friction μeff of the granular material as a function of particle elongation from DEM simulations with spherocylinders with particle friction of μp=0.4, 0.2 and 0.1 [4]. (b) Shear torque as a function of grain aspect ratio obtained in laboratory experiments by quasistatic shearing of a granular material consisting of plastic (POM - Polyoxymethylene) ellipsoids [5]. |
Silo flow and clogging
Considering flow in an hourglass or silo discharge, we can ask how the grain shape affects the flow rate, or – for small orifice size – the clogging probability of the granular material. As for the flow rate, we again observe a non-monotonic curve both in DEM simulations and in laboratory experiments (Fig. 5). We find that slightly elongated or slightly flat particles discharge faster than spherical or more anisometric particles [5]. This sounds like a contradiction, since – as we described above – in a shear flow exactly those particles showed the strongest resistance against shearing.
 |
Fig. 5: Silo flow rate as a function of grain aspect ratio for granular materials with various grain shapes [5]. All grains have the same volume, equivalent to the volume of a sphere with diameter d*. The curves with different colors correspond to different normalized orifice sizes D/d*. |
In order to resolve this apparent contradiction we should consider the following: the packing fraction of ellipsoids (both in a random configuration as well as during shear flow) is a similar non-monotonic function of aspect ratio as the flow rate [5,6]. Thus, since we have more grains per unit volume for slightly elongated or slightly flat particles than for spheres or for very anisometric grains, it is actually not so much surprising that we get larger silo flow rate and at the same time we also get larger resistance of those materials against shear deformation. This last aspect is strongly related to the anisotropy and distribution of interparticle contact forces in the system [7,8].
Finally, for comparing the clogging probability for different grain shapes, researchers measure the typical orifice size above which no clogging occurs [9,10]. This is done by measuring the number of grains leaving the silo between subsequent clogs. This quantity rapidly increases (apparently diverges) at a critical orifice size Dc. In Fig. 6 we see that Dc strongly increases with grain aspect ratio, indicating increased clogging probability for more elongated grains. This aspect is not yet explored for moderately elongated particles (around the aspect ratio of 2), thus it is not yet known whether the clogging probability is also a non-monotonic function of aspect ratio in that range of grain aspect ratios.
 |
Fig. 6: (a) A reconstructed clogged state of elongated particles in a silo based on X-ray tomographic measurement [11]. (b) Normalized critical orifice size Dc/d* vs. grain aspect ratio [9,10]. Above Dc practically no clogging occurs. Here again d* is the equivalent diameter of the particle, which corresponds to the diameter of a sphere with the same volume as the particle. |
About the Author

Tamás Börzsönyi is senior researcher at the HUN-REN Wigner Research Centre for Physics (Budapest, Hungary). His main research interests are related to granular materials, complex fluids, liquid crystals and non-linear phenomena.
Acknowledgements
Collaboration with E. Somfai, B. Fan, T. Pongó, D.B. Nagy, P. Claudin, R.C. Hidalgo, A. Ashour and R. Stannarius is warmly acknowledged.
References
- B. Andreotti, Y. Forterre and O. Pouliquen, Granular Media: Between Fluid and Solid, Cambridge Univ. Press, Cambridge UK, (2013) [Google Scholar]
- G.B. Jeffery, Proceedings of the Royal Society Series A 102, 161 (1922) [Google Scholar]
- T. Börzsönyi, B. Szabó, G. Törös, S. Wegner, J. Török, E. Somfai, T. Bien, and R. Stannarius, Phys. Rev. Lett. 108, 228302 (2012) [Google Scholar]
- D.B. Nagy, P. Claudin, T. Börzsönyi and E. Somfai, New J. Phys. 22, 073008 (2020) [Google Scholar]
- B. Fan, T. Pongó, R. Cruz Hidalgo and T. Börzsönyi, Phys. Rev. Lett. 133, 058201 (2024) [Google Scholar]
- A. Donev, I. Cisse, D. Sachs, E.A. Variano, F.H. Stillinger, R. Connelly, S. Torquato, and P.M. Chaikin, Science 303, 990 (2004) [Google Scholar]
- E. Azéma and F. Radjai, Phys. Rev. E 81, 051304 (2010), and Phys. Rev. E 85, 031303 (2012) [Google Scholar]
- M. Boton, E. Azéma N. Estrada, F. Radjai and A. Lizcano, Phys. Rev. E 87, 032206 (2013) [Google Scholar]
- I. Zuriguel, A. Garcimartín, D. Maza, L.A. Pugnaloni and J. M. Pastor, Phys. Rev. E 71, 051303 (2005) [Google Scholar]
- A. Ashour, S. Wegner, T. Trittel, T. Börzsönyi, and R. Stannarius, Soft Matter 13, 402 (2017) [Google Scholar]
- V. Nagy, B. Fan, E. Somfai, R. Stannarius and T. Börzsönyi, J. Stat. Mech. 113201 (2023) [Google Scholar]
All Figures
 |
Fig. 1: (a) Schematic view of a granular material consisting of spherocylinders exposed to simple shear in a pressure controlled Discrete Element Model (DEM) calculation and (b) sketch of the cylindrical split bottom shear cell, in which the granular material is slowly sheared in the shear zone (indicated with red color). |
| In the text | |
 |
Fig. 2: Illustration of the rotation (tumbling) of an ellipsoidal particle in a liquid which is exposed to laminar shear flow with smooth (linear) velocity profile. |
| In the text | |
 |
Fig. 3: (a) Orientation distribution of rice grains with different aspect ratio obtained in shear experiments. (b) Average angle of elongated particles as a function of particle aspect ratio in a dense granular shear flow [3]. Experimental data obtained on the surface of the granular layer or inside by X-ray computed tomography (CT). |
| In the text | |
 |
Fig. 4: (a) Effective friction μeff of the granular material as a function of particle elongation from DEM simulations with spherocylinders with particle friction of μp=0.4, 0.2 and 0.1 [4]. (b) Shear torque as a function of grain aspect ratio obtained in laboratory experiments by quasistatic shearing of a granular material consisting of plastic (POM - Polyoxymethylene) ellipsoids [5]. |
| In the text | |
 |
Fig. 5: Silo flow rate as a function of grain aspect ratio for granular materials with various grain shapes [5]. All grains have the same volume, equivalent to the volume of a sphere with diameter d*. The curves with different colors correspond to different normalized orifice sizes D/d*. |
| In the text | |
 |
Fig. 6: (a) A reconstructed clogged state of elongated particles in a silo based on X-ray tomographic measurement [11]. (b) Normalized critical orifice size Dc/d* vs. grain aspect ratio [9,10]. Above Dc practically no clogging occurs. Here again d* is the equivalent diameter of the particle, which corresponds to the diameter of a sphere with the same volume as the particle. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


