Identifying ever-growing disturbances leading to freak waves (Vol. 46 No. 5-6)
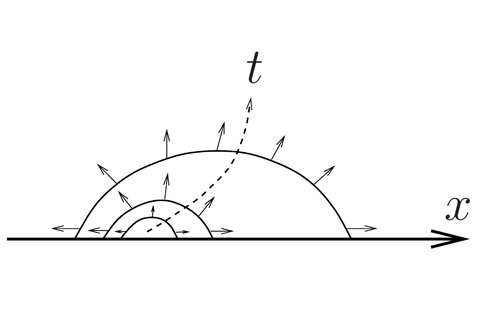 A schematic one-dimensional illustration of the spatiotemporal evolution of the envelope of wave-train in the absolutely unstable case.
A schematic one-dimensional illustration of the spatiotemporal evolution of the envelope of wave-train in the absolutely unstable case.
Physicists now better understand wave systems exhibiting unusual disturbances by identifying growing localised patterns as early indicators of such disturbances.
Physicists like to study unusual kinds of waves, like freak waves found in the sea. Such wave movements can be studied using models designed to describe the dynamics of disturbances. The authors have focused on finding ways of best explaining how wave disturbance occurs under very specific initial conditions that are key to the genesis of these disturbances. They looked for solutions to this puzzle by resolving a type of equation, called the nonlinear Schrödinger equation. It is solved by applying a method designed for studying instabilities tailored to these initial conditions. Their approach makes it possible to locate exactly where and how pertinent information used to identify disturbance patterns can be extracted from localised disturbances' characteristics. The findings have been published recently. They therefore contribute to a better understanding of the complex dynamics of systems subjected to such disturbances. For example, they could be used to better understand waves appearing on fluid surfaces, whose evolution is influenced by gravity, or light waves propagated in optical fibres.
S. Coulibaly, E. Louvergneaux, M. Taki and L. Brevdo, Spatiotemporal wave-train instabilities in nonlinear Schrödinger equation: revisited, Eur. Phys. J. D 69, 186 (2015)
[Abstract]






