Delayed dynamic triggering of earthquakes (Vol. 42, No. 5)
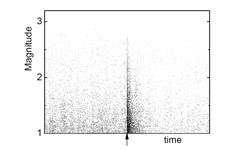 Magnitude-time plot of quakes in the model. At the time of the arrow an instantaneous perturbation is applied. Note the resulting increase in activity.
Magnitude-time plot of quakes in the model. At the time of the arrow an instantaneous perturbation is applied. Note the resulting increase in activity.
In recent years, evidence has been accumulating that seismic waves generated by a large earthquake can produce additional quakes far away of the main shock. This may not be surprising when the secondary quakes occur right at the occurrence of the seismic waves. However, in general these dynamically triggered earthquakes occur hours or days after the main shock, namely when the seismic waves have elapsed.
In order to understand the origin of this phenomenon, we have adapted a recently proposed statistical model of seismicity that takes into account the existence of plastic relaxation processes within the faults. This kind of model has been used before to obtain realistic sequences of earthquakes, including in particular aftershocks. By appropriately defining a perturbation (assumed to be the occurrence of seismic waves), it is observed that the seismic activity in the system has a sharp increase following the perturbation, well after it has vanished.
The origin of a temporarily delayed effect in the model is tightly related to the existence of relaxation processes, as the effect does not exist in the case in which relaxation is absent. In this respect delayed dynamically triggered earthquakes are in some sense similar to aftershocks: the latter are delayed events triggered by a permanent perturbation (the change in the stress field caused by the main shock) while the former are delayed events triggered by a transient perturbation (the passage of seismic waves), once the perturbation has vanished.
The present investigation suggests that both aftershocks and delayed dynamically triggered quakes originate in the same kind of physical mechanism, namely internal relaxation mechanisms within the faults, that the present model appropriately captures.
Delayed dynamic triggering of earthquakes: Evidence from a statistical model of seismicity
E. A. Jagla, EPL 93 19001 (2011)
[Abstract]






