Eigenvalue problem in 2D for an irregular boundary (Vol. 42, No. 5)
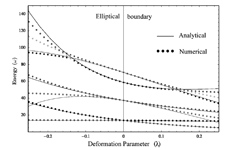 Comparison of the eigenvalues obtained numerically and analytically for an elliptical boundary (in units of 1/Ro2) with Neumann condition for the first 7 states.
Comparison of the eigenvalues obtained numerically and analytically for an elliptical boundary (in units of 1/Ro2) with Neumann condition for the first 7 states.
The Helmholtz equation arises in a number of physical contexts as one reduces the wave equation by considering single frequency propagation. One such application appears in studying wave behaviour in waveguides. While waveguides in technology are carefully engineered to have, for instance, constant and simple cross-sectional geometries, natural waveguides relax such engineering constraints. (Natural waveguides range across systems from atmospheric and oceanic ducts, to biological systems such as seal and polar bear hair fibres.) In particular the cross section of natural waveguides tends to have a complex boundary shape that is far from the ideal circular or rectangular form of engineered waveguides.
The present team proposes a new approach to the irregular boundary 2-d Helmholtz equation with Neumann boundary conditions (specified normal derivatives of the field at the boundary). This boundary condition has significant physical importance: it is the natural one for electromagnetic propagation in the TM mode in waveguides.
To date the most successful efforts to solve the irregular boundary Helmholtz equation have been computational, but even this general method has its drawbacks. The present analytic perturbative approach solves the irregular boundary problem via a perturbative series. The authors explicitly work out several nontrivial examples. The benefits of this approach include, most importantly, an analytical understanding of the behaviour of the solution as the amplitude of the boundary distortion is increased.
Another important feature of Panda et al.’s expression is its analytic precision in the terms computed and its analytic error estimates for the terms truncated from the series. Together these give the analytic methods a much larger dynamic range than available computationally.
Eigenvalue problem in two dimensions for an irregular boundary: Neumann condition
S. Panda, S. Chakraborty, and S.P. Khastgir, Eur. Phys. J. Plus, 126, 62 (2011)
[Abstract]






