Statistical physics approach to graphical games (Vol. 42, No. 3)
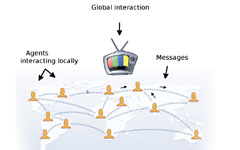 network of agents playing a graphical game. The payoff matrices depend both
on the local neighbourhoods and on some aggregate signal. The equilibriums
are reached by exchanging localmessages and their overall geometrical structure
can be analyzed by statistical physics techniques.
network of agents playing a graphical game. The payoff matrices depend both
on the local neighbourhoods and on some aggregate signal. The equilibriums
are reached by exchanging localmessages and their overall geometrical structure
can be analyzed by statistical physics techniques.
A graphical game is a mathematical framework to analyse strategic interactions among self-interested agents who play only with their neighbours in a graph. It usually makes predictions in terms of equilibrium concepts, chief among which is the Nash equilibrium: a configuration of strategies where nobody has a unilateral incentive to deviate. The problem of finding a Nash equilibrium is believed to be computationally intractable. In this work we show how to use methods from statistical physics of disordered systems to develop efficient and fully distributed (approximate) algorithms to tackle this problem. Furthermore, motivated by the recent interest in the study of the interplay between local and global interactions in multi-agent systems, we propose a new compact representation of games that extends over graphical games to deal conveniently with a global interaction and show how to extend the methods to this new case. We also derive the phase diagrams of different ensembles of random graphical games and study the structure of the corresponding space of solutions. Evidence of HARD/EASY phase transitions is found in some cases.
Statistical physics approach to graphical games: local and global interactions
A. Ramezanpour et al., Eur. Phys. J. B 80, 555 (2011)
[Abstract]





