Mean-field theory and stochastic evolution (Vol. 42, No. 2)
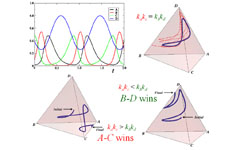 Opposing pairs (A-C, B-D) of equal strength evolve deterministically on a closed orbit (blue loop), oscillating endlessly (upper left). An example of stochastic trajectories is shown in red (dashed line). Lower panels display systems with identical initial conditions but different strengths, ending at opposite edges.
Opposing pairs (A-C, B-D) of equal strength evolve deterministically on a closed orbit (blue loop), oscillating endlessly (upper left). An example of stochastic trajectories is shown in red (dashed line). Lower panels display systems with identical initial conditions but different strengths, ending at opposite edges.
Population dynamics is a venerable and widely applicable subject. Over the last two centuries, many studies provided valuable insights into various phenomena, e.g., the emergence of biodiversity and fitness/extinction, while novelties are continually being discovered. Specifically, recent investigations of three species competing cyclically (e.g., rock-paper-scissors game) revealed rich and complex behaviours, whether the populations are well-mixed or dwelling on one- or two-dimensional lattices. Indeed, the well-mixed system displayed surprising survival probabilities: The species with the slowest consumption rate wins, leading to a popularized headline "Survival of the Weakest." Fascinating properties were also found in systems with spatial structure, including formation of complex patterns and mobility effects. Many aspects can be understood by exploiting techniques from statistical physics and non-linear dynamics.
Our work focuses on four cyclically competing species. Unlike the 3-species case, ours allows final states with coexisting pairs. The reason is simple: Resembling the game of Bridge, the four form two opposing teams of ally-pairs. For each pair, the product of their consumption rates determines if it wins or loses. From a master equation for the full stochastic problem, we derive an approximate set of rate equations (ODE's). Predictions from the latter typically agree well with simulations. Instead of the weakest surviving, our observations support a different maxim: "The prey of the prey of the weakest is the least likely to survive." Intuitively reasonable, this principle also applies to the special 3-species case! Meanwhile, a variety of intriguing extinction probabilities, discovered through simulations, provides numerous challenges for future research.
Cyclic competition of four species: Mean-field theory and stochastic evolution
S. O. Case, C. H. Durney, M. Pleimling and R. K. P. Zia, EPL, 92, 58003 (2010)
[Abstract] | [PDF]







