Fractal agglomerates fragment into dissimilar fragments (Vol. 50, No. 5-6)

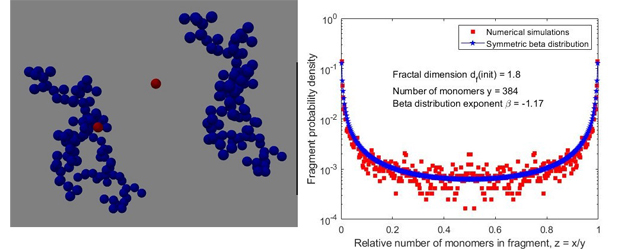
Fragmentation occurs everywhere in nature: polymers degrade, soot particles break up, cells divide, volcanic ash fragments, droplets break up in turbulent flow, lung fluid fragments to generate droplets. Nevertheless, little is known about the distribution of fragment sizes when a fractal agglomerate breaks up. The fragment-size distribution upon random bond removal in a linear chain composed of identical units is uniform. How does the distribution change as the morphology of the fragmenting structure changes?

More generally, fragmentation kernels, which depend on the size distribution and the fragmentation rate, have been extensively used in population balance equations. Usually, their analytical form is dictated by homogeneity requirements (as suggested by coagulation kernels) or physical arguments. In this work, the morphology-dependent fragment-size distribution is determined from numerical simulations of fragmenting in silico fractal-like agglomerates. The overarching idea is to map the agglomerate onto a graph via the adjacency matrix, the matrix that specifies the monomer-monomer bonds. Fragmentation occurs via random bond removal. The simulations showed that the distribution is U-shaped, fragmentation into dissimilar fragments, accurately reproduced by a symmetric beta distribution.

Y. DrossinoS, A. D. Melas, M. Kostoglou and L. Isella, Morphology-dependent random binary fragmentation of in silico fractal-like agglomerates, EPL 127, 46002 (2019)
[Article]