Accueil
Pionic Deuterium (Vol. 42, No. 5)
A new precise measurement of the pD(3p-1s) X-ray transition in the pionic deuterium atom has been performed at the PSI accelerator in Switzerland. The pionic deuterium is a short lifetime atom, where the negative pion (p-) replaces the electron, resulting in an atomic size scaled down by the ratio of the pion mass over electron mass, a factor of about 270.
The experiment makes use of a high intensity decelerated beam of - stopping in a cooled deuterium gas target where the p- is captured. Following the capture an atomic de-excitation quantum cascade of 0.1ns duration takes place and the atom ends up in the 1s ground state as shown in the Figure. A Bragg spectrometer equipped with a bent Silicon crystal and pixel semiconductor detectors provides the precise X-ray detection in the appropriate keV region.
The measurement of the energy of the X-ray emitted in the pD(3p-1s) transition leads to a new value of 3075.583 ± 0.030 eV. A new and updated calculation of this transition energy assuming a pure electromagnetic system (pure QED - no strong interaction) leads to a value of 3077.939 ± 0.008 eV. The difference between these two quantities gives exactly the hadronic shift e1s = -2.336 ± 0.031 eV. The line-shape has been analysed, providing a new and precise value of the hadronic broadening G1s = 1.171+0.023 -0.049 eV.
The accuracy of 1.3% achieved for the shift e1s leads to a more precise determination of the isoscalar scattering length a+ (pD being an isoscaler object). The new precise value obtained for the hadronic broadening G1s leads to a new determination of the threshold parameter a, the transition strenght for a S-wave pion, with unprecedented accuracy.
Pionic Deuterium
Th. Strauch, F.D. Amaro, D.F. Anagnostopoulos, P. BÅNuhler, D.S. Covita, H. Gorke, D. Gotta, A. Gruber, A. Hirtl, P. Indelicato, E.-O. Le Bigot, M. Nekipelov, J.M.F. dos Santos, Ph. Schmid, S. Schlesser, L.M. Simons, M. Trassinelli, J.F.C.A. Veloso and J. Zmeskal, Eur. Phys. J. A, 47, 88 (2011)
[Abstract]
Electromagnetic force density and energy-momentum tensor in any continuous medium (Vol. 42, No. 5)
For more than a century, physicists have searched for a unique and general form for the force density that an electromagnetic field imposes on a medium. The existing expressions for this quantity, obtained, e.g., by Minkowski, Einstein and Laub, Abraham, and Helmholtz, are different, and, as such, give different predictions in particular physical situations. The theories of Abraham and Minkowski, for example, ignore the existence of electro- and magnetostriction. Moreover, real media with dispersion, dissipation, and nonlinearities have not been addressed much.
We present an unambiguous general equation for the electromagnetic force density f = -∇T- (dG/dt) expressed in terms of a new three-dimensional energy-momentum tensor T and momentum density G of the field. The tensor T can be written as T = TM + IV, where TM is the Minkowski tensor, I the unit tensor, and V the density of the field-matter interaction potential that is responsible for electro- and magnetostriction. Remarkably, if the medium is not magnetic, the momentum density G is given by Abraham’s expression G = ExH/c2. If the material obeys the Clausius-Mossotti law, the tensor T becomes the Helmholtz tensor that to our knowledge has not been contradicted in any experiment so far.
The general equation obtained for the force density can be applied to essentially any natural or designed material whether inhomogeneous, anisotropic, nonlinear, dispersive, or dissipative, and even to materials providing optical gain. We also calculate the rate of work done on a medium by an electromagnetic field, and using the result, obtain the four-dimensional energy-momentum tensor T4 in spacetime. Interestingly, this tensor is physically very close to the almost forgotten tensor of Einstein and Laub.
Electromagnetic force density and energy–momentum tensor in an arbitrary continuous medium
A. Shevchenko and M. Kaivola, J. Phys. B: At. Mol. Opt. Phys. 44, 175401 (2011)
[Abstract]
XUV-FEL spectroscopy: He two-photon ionization cross-sections (Vol. 42, No. 5)
Non-linear optical processes of atoms and molecules such as multiphoton absorption and tunnelling ionization are very attractive issues in current atomic, molecular and optical sciences. The recent development of free electron laser (FEL) sources enabled us to investigate such non-linear optical processes in the extreme ultraviolet (XUV) wavelength regions Our group demonstrated that we can determine absolute values of a two-photon ionization cross section of atomic species and its wavelength dependence by using an XUV FEL light source. This was achieved by introducing an internal reference for the cross section measurements and by the frequency tunability of the FEL light source.
The FEL light source we used is the SPring-8 Compact SASE Source test accelerator in RIKEN, Harima Institute, equipped with a couple of compact vacuum undulators, having a unique advantage of its high peak intensity and frequency tunability in the 50 ~ 62 nm region.
We measured the wavelength dependence and the light field intensity dependence of the absolute values of two-photon ionization cross section of He at 53.4, 58.4, 56.0 and 61.4 nm, covering the 1s2p and 1s3p resonances in the light field intensities range of 5×1012 ~ 5×1013 W/cm2 by measuring simultaneously one-photon ionization signal of H2 mixed in the sample as reference.
We showed through the critical comparison with the theoretically obtained cross sections that, in the resonance wavelength regions, dressed state formation through the strong coupling between the intermediate 1snp resonance state and the 1s2 ground state needs to be taken into account if the XUV light field intensity becomes larger than ~1012 W/cm2. We are now entering into the stage of quantitative non-linear spectroscopy in the XUV wavelength region.
Determination of absolute two-photon ionization cross section of He by XUV Free Electron Laser
T. Sato, A. Iwasaki, I. Kazuki, T. Okino, K. Yamanouchi, J. Adachi, A. Yagishita, H. Yazawa, F. Kannari, M. Aoyma, K. Yamakawa, K. Midorikawa, H. Nakano, M. Yabashi, M. Nagasono, A. Higashiya and T. Ishikawa, J. Phys. B: At. Mol. Opt. Phys., 44, 161001 (2011)
[Abstract]
Eigenvalue problem in 2D for an irregular boundary (Vol. 42, No. 5)
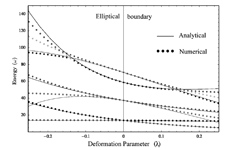 Comparison of the eigenvalues obtained numerically and analytically for an elliptical boundary (in units of 1/Ro2) with Neumann condition for the first 7 states.
Comparison of the eigenvalues obtained numerically and analytically for an elliptical boundary (in units of 1/Ro2) with Neumann condition for the first 7 states.
The Helmholtz equation arises in a number of physical contexts as one reduces the wave equation by considering single frequency propagation. One such application appears in studying wave behaviour in waveguides. While waveguides in technology are carefully engineered to have, for instance, constant and simple cross-sectional geometries, natural waveguides relax such engineering constraints. (Natural waveguides range across systems from atmospheric and oceanic ducts, to biological systems such as seal and polar bear hair fibres.) In particular the cross section of natural waveguides tends to have a complex boundary shape that is far from the ideal circular or rectangular form of engineered waveguides.
The present team proposes a new approach to the irregular boundary 2-d Helmholtz equation with Neumann boundary conditions (specified normal derivatives of the field at the boundary). This boundary condition has significant physical importance: it is the natural one for electromagnetic propagation in the TM mode in waveguides.
To date the most successful efforts to solve the irregular boundary Helmholtz equation have been computational, but even this general method has its drawbacks. The present analytic perturbative approach solves the irregular boundary problem via a perturbative series. The authors explicitly work out several nontrivial examples. The benefits of this approach include, most importantly, an analytical understanding of the behaviour of the solution as the amplitude of the boundary distortion is increased.
Another important feature of Panda et al.’s expression is its analytic precision in the terms computed and its analytic error estimates for the terms truncated from the series. Together these give the analytic methods a much larger dynamic range than available computationally.
Eigenvalue problem in two dimensions for an irregular boundary: Neumann condition
S. Panda, S. Chakraborty, and S.P. Khastgir, Eur. Phys. J. Plus, 126, 62 (2011)
[Abstract]









