Accueil
Plasmas as gaseous electrodes for aqueous electrochemistry (Vol. 44 No. 1)
 Atmospheric-pressure microplasma stably formed in a flow of argon gas at the surface of acidic water
Atmospheric-pressure microplasma stably formed in a flow of argon gas at the surface of acidic water
Plasmas are ionized gases made-up of electrons and gaseous ions. In theory, plasmas are a source of charge that can be coupled with liquids to initiate electrochemical reactions in solution. This has been known for some time, at least since 1887 when Gubkin first reported the use of plasmas for electroplating silver from silver nitrate. Unfortunately, plasmas are inherently difficult to stabilize at atmospheric pressure, and vacuum operation has limited prior experiments to solvents with low vapour pressures such as ionic liquids.
The present work shows how to get stable atmospheric-pressure plasmas allowing aqueous electrochemical reactions. The approach is based on pd scaling (gas pressure p and dimension d of the plasma) which imposes to reduce the dimension of the plasma to go to higher pressure. Atmospheric operation is achieved by forming a µm-scale plasma, or microplasma.
Upon operating the microplasma as the cathode at the surface of an aqueous solution, the electrons from the plasma reduce the protons to produce hydrogen gas. At the platinum counter-electrode, oxidation reactions lead to the formation of oxygen gas. The electrolysis of water is well known in electrochemistry, but this is the first time it has been demonstrated with a plasma electrode. As plasmas are increasingly in use with wet electrodes for medical and materials applications, it is crucial to understand the high complexity of plasma-liquid interactions. The role of electrons has thus far been largely overlooked, and this work brings a crucial piece of the puzzle.
M. Witzke, P. Rumbach, D. B. Go and R. M. Sankaran, ’Evidence for the electrolysis of water by atmospheric-pressure plasmas formed at the surface of aqueous solutions’, J. Phys. D 45, 442001 (2012)
[Abstract]
Droplet production for electrolyte solutions (Vol. 44 No. 1)
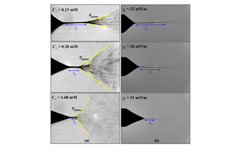 The micro-jet length Lj and nanoaerosol plume angle θplume are observed to be strong functions of the ionic strength C∞ and interfacial tension γf.
The micro-jet length Lj and nanoaerosol plume angle θplume are observed to be strong functions of the ionic strength C∞ and interfacial tension γf.
Proteomic mass spectrometry and chemical imaging require the generation of nanometer-sized charged water drops that are emitted in a precise direction. This is done with the remarkable ability of an electric field to sharpen a mm-sized spherical drop into a sharp cone with a universal half angle of 49 degrees, to emit a micro-jet at the cone tip and to breakup the charged micro-jet explosively into a plume of nanodrops, whose plume angle and charge per drop sensitively affect the measurement accuracy of the instrument. This paper captures the underlying nanoscale physics of DC electrospray with a combination of strong electrolyte theory, electrostatics, interfacial phenomena and potential spectral theory for geometric singularities. The electric field of the most singular harmonic near a cone that sharpens the drop is also shown to charge a nanoscale capacitor at the interface of the micro-jet, with a dimension of the Debye length. The interfacial charging increases downstream of the cone tip until the space charge separation is below the Bjerrum length, when the repulsive Coulombic energy between two charges exceeds the thermal energy. The resulting Coulombic fission accounts for the explosive breakup of the micro-jet into the nanodrop plume. The micro-jet length, the charge per nanodrop and the nanodrop plume angle as functions of ion strength are accurately captured by the theory as functions of the ionic strength and surface tension. Strong ionic strength and low surface tension produce the longest micro-jet, the smallest plume and the most precisely directed nanodrops.
Y. Wang, M. K. Tan, D. B. Go and H-C. Chang, ‘Electrospray cone-jet breakup and droplet production for electrolyte solutions’, EPL, 99, 64003 (2012)
[Abstract]
Replica techniques can predict learning curves (Vol. 44 No. 1)
 Predicted mean square errors vs number of examples per vertex, for different noise levels σ2 (triangles), agree very well with numerical simulations (circles, graphs with 500 vertices) and improve significantly on existing approximations (dashed line).
Predicted mean square errors vs number of examples per vertex, for different noise levels σ2 (triangles), agree very well with numerical simulations (circles, graphs with 500 vertices) and improve significantly on existing approximations (dashed line).
We show that statistical physics approaches, in particular the replica method, can be used to accurately predict the learning curve of a Gaussian process (GP) inferring a function from noisy data, for a wide range of discrete input spaces. The learning curve quantifies performance as average mean square error versus number of training examples.
GPs are a popular Bayesian inference technique. A GP prior is placed over a function space, and combined with the likelihood of the observed data given a function. Bayes’ theorem then gives a posterior distribution over functions. For a likelihood describing Gaussian noise corrupting the observed function values, this is again a GP, which can be used to make predictions about the function. GPs are “non-parametric”: they effectively represent functions with infinitely many parameters. This makes analysis of their learning curves non-trivial, and much has been achieved for GPs learning functions whose inputs are real-valued. However, predictions are generally only qualitatively correct, with exact solutions only for special cases. We show for the case where inputs are discrete, specifically vertices on a random graph, that replica techniques can be used to predict learning curves exactly in the limit of large graphs.
The starting point is to represent the average error as the derivative of a partition function. We rewrite this so that only neighbouring vertices are directly coupled. From here one can apply the replica method to find the required quenched average over the randomness in the data set. The results apply to random graph ensembles constrained by any fixed degree distribution, and can be generalised to more complicated ensembles.
M. J. Urry and P. Sollich, ‘Replica theory for learning curves for Gaussian processes on random graphs’, J. Phys. A: Math. Theor. 45, 425005 (2012)
[Abstract]
Conjugate Fermi hole and the first Hund rule (Vol. 44 No. 1)
 Structure of the genuine and conjugate Fermi holes in the internal space for the (1s)(2p) singlet-triplet pair of states of He-like systems: (a) – (c) correspond to the nuclear charge Zn of 20, 5, and 2, respectively. (a’) – (c’) represent the electron repulsion potential for the corresponding Zn.
Structure of the genuine and conjugate Fermi holes in the internal space for the (1s)(2p) singlet-triplet pair of states of He-like systems: (a) – (c) correspond to the nuclear charge Zn of 20, 5, and 2, respectively. (a’) – (c’) represent the electron repulsion potential for the corresponding Zn.
Empirically derived Hund's rules of the pre-quantum-mechanics era predict the ordering of the energy levels possessing different spin and orbital angular momentum quantum numbers. They have proved to be almost universally valid for atoms, molecules, and quantum dots. Yet, despite of a long-standing debate, the search for their origin persists primarily due to the lack of the precise knowledge of the electronic structure in different spin states. We explore the origin of the first Hund rule for a two-dimensional model of He-like systems and that of two-electron quantum dots. They represent ideal systems providing a direct fundamental insight into the structure of the internal part of the fully correlated wave functions, allowing an unambiguous argument.
An examination of their probability density distributions reveals indeed the existence of a region in the internal space, which we refer to as a conjugate Fermi hole. In this region the singlet wave function has a smaller probability density than the corresponding triplet one, in contrast to the genuine Fermi hole where the triplet has a smaller density than the singlet. Due to the presence of this conjugate Fermi hole the singlet probability density has to migrate far away from the centre of the one-electron potential. This rationalizes the well-known broader electron density distribution of the singlet state relative to the corresponding triplet. This key observation explains the singlet-triplet energy gap.
T. Sako, J.Paldus, A. Ichimura and G. H. F. Diercksen, ‘Origin of the first Hund rule and the structure of Fermi holes in two-dimensional He-like atoms and two-electron quantum dots’, J. Phys. B: At. Mol. Opt. Phys. 45, 235001 (2012)
[Abstract]







